LEC 1 概述

解决问题的三要素：输入输出算法

数据结构

输入、输出与数据结构直接相关。

数据结构时数据之间的逻辑关系、数据在计算机上的存储方式、数据的操作。

数据结构与算法设计是密切相关的。

算法

算法是为了求解问题而给出的指令序列。

一般特性

正确性有效性确定性有穷性

算法效率

计算时间存储空间网络带宽

LEC 2 算法渐进分析

一般我们不必花大力气算出算法的精确运行时间，我们关心的是在大规模的输入下，算法的运行时间是如何随着输入规模的增大而变化的。此时，我们可以忽略低阶项和常量，使用渐进分析。开销函数的估计是相对的而不是绝对的，开销函数的阶的增长决定了开销的大小。

渐进符号

$O$ 渐进上界 $Ω$ 渐进下界 $Θ$ 渐进紧确界

分析实例

矩阵求和

$O(n)$ $n=k^2$ （k 为矩阵维度）

插入排序

最好 O(n) 最坏 O(n^2)

合并排序

$O(nlgn)$

LEC 3 递归关系

许多算法，时间开销函数都可以用递归关系来描述。

置换法

猜想出一个表达式，验证表达式的正确性。

递归树

将迭代过程展成树的形式，分析树的每一层的消耗，然后求和。

迭代法

根据迭代公式，利用数学方法求解。

主方法

主方法依赖如下的主定理：

可以根据主定理方便求解效率，但有真空地带。

LEC 4 线性时间的排序法

基于比较的排序的开销下限

这一节先分析了基于比较的方法的排序的开销下限，我们通过判定树模型证明下限为$nlgn$。要打破这个下限，就要寻找非比较的排序方法，即：

计数排序

基本思想是排序指定范围内（0~k）的数，使用大小分别为n、k、n的数组a、b、c。根据 c 中小于 x 的个数，将元素放到 b 的指定位置。

基数排序

基本思想是根据数字每一位的大小进行排序。

桶排序

基本思想是将待排序元素放入桶中，每个桶分别排序，桶之间保持顺序。

LEC 5 分治法

分治法的思想，将原问题分解为几个规模较小但类似于原问题的子问题，递归地求解这些子问题，然后再合并这些子问题的解来建立原问题的解。

分治模式在每层递归时的三个步骤：

分解步骤将问题划分为一些子问题，子问题的形式与原问题一样，只是规模更小。

解决步骤递归的求解子问题，如果子问题的规模足够小，则停止递归直接求解。

合并步骤将子问题的解组合成原问题的解。

应用

二分搜索

归并排序

最大子数组问题

矩阵乘法的 Strassen 算法

Strassen 算法的运行时间的递归式为：

$T(n)=7T(n/2)+Θ(n^2)$

这里 a=7，b=2，$f(n)=Θ(n^2)$，即$n^{log_ba}=n^{log_27}$。存在ε=0.8有$f(n)=O(n^{lg7-ε})$。符合主定理的情况1，则$T(n)=Θ(n^{lg7})$。

LEC 6 随机化算法

雇佣关系

快速排序

随机化算法的分类

Las Vegas 算法：总能给出正确的解或者无解。

Monte Carlo 算法：大多数给出正确解，错误率可以控制在一定程度上。

如检查两个长串是否相同，直接比较为 Las Vegas 算法，验证指纹则为 Monte Carlo 算法。

LEC 7 统计算法

LEC 8 动态规划

简介

动态规划（dynamic programming），这里的 programming 不是编程的意思，而是表格的意思，意味着将求出的子问题的解存到表格中，以便下次用到时直接查表取出。动态规划与分治法类似，都是通过组合子问题的解来求解原问题。是典型的以空间换取时间的时空权衡的例子。

原理

适合用动态规划求解的问题的两个要素：最优子结构和子问题重叠。

步骤

动态规划求解的一般步骤：

（1）刻画一个最优解的结构特征。

（2）递归地定义最优解的值。

（3）计算最优解的值，通常采用自底向上的方法。

（4）利用计算出的信息构造一个最优解。

应用

动态规划有着很规范的范式，一般按照步骤来。

最长公共子序列

刻画最长公共子序列的特征

我们很容易用“剪切-粘贴”技术证明：两个序列的 LCS 包含这两个序列前缀的 LCS。即 LCS 问题拥有最优子结构。

一个递归解

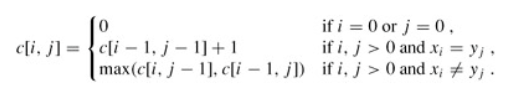
计算 LCS 的长度

我们使用两个表 c 和 b。

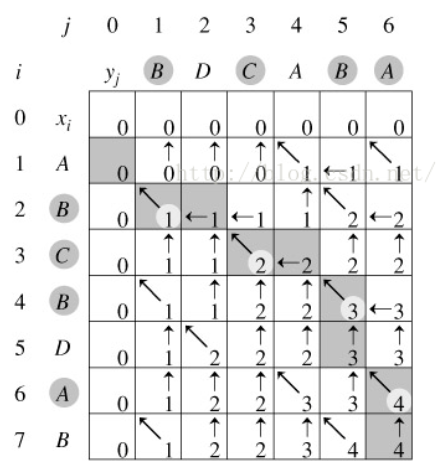
Snipaste_2020-05-05_18-20-06

构造 LCS

沿着表 b 的箭头方向，从右下角开始，打印出公共元素即可。

作业排程

钢条切割

矩阵链乘法

矩阵链乘法就是寻找一个最优括号化方案，使得需要的标量乘法计算次数最少。

最优括号化方案的结构特征

最优括号化方案拥有最优子结构，我们可以使用“剪切-粘贴”方法很容易得证明，最优括号化方案包含其子链的最优括号化方案。

一个递归求解方案

计算最优代价

伪代码：

MATRIX-CHAIN-ORDER(p)
n = p.length-1
let m[1..n 1..n] and s[1..n-1,2..n] be new table
for i = 1 to n
    m[i,i] = 0
for l = 2 to n
    for i = 1 to n-l+1
        j = i+l-1
        m[i,j] = ∞
        for k = i to j-1
            q = m[i,k] + m[k+1,j] + p[i-1] * p[k] * p[j]
            if q < m[i,j]
                m[i,j] = q
                s[i,j] = k
return m and s

构造最优解

设计一个算法输出括号化方案。

LEC 9 贪心算法

简介

贪心算法和动态规划算法一样，通常用来求解最优化问题。

贪心算法的思想是每一步都选择局部最优解，很多时候这种方法能得到最优解，而且速度比动态规划快很多，也更简单。

原理

并没有确定的方法简单证明一个问题是否适用贪心算法。

但贪心选择性质和最优子结构是两个关键要素。

步骤

（1）将最优化问题转化为这样的形式：对其做出一次选择后，只剩下一个子问题需要求解。

（2）证明作出贪心选择后原问题总是存在最优解。即贪心选择总是安全的。

（3）证明做出贪心选择后剩余的子结构满足性质：其最优解与贪心选择组合即可得到原问题的最优解，这样就得到了最优子结构。

应用

活动选择问题

霍夫曼编码

最小生成树

单源最短路径的 Dijkstra 算法

LEC 10 图算法

图的表示和存储方式

邻接链表邻接矩阵

邻接链表因为在表示稀疏图时非常紧凑而成为通常的选择。

在稠密图的情况下，我们可能倾向于使用邻接矩阵表示法。快速判断任意两个节点之间是否有边相连，可能也需要使用邻接矩阵表示法。

LEC 11 最小生成树

LEC 12 单源最短路径

单源最短路径

单源最短路径问题是从源结点到其它结点的最短路径问题。

一般解决方案是 Bellman-Ford 算法，其允许负值权重的边。当存在负值环路时，算法返回不存在问题的解，否则返回最短路径及权重。思想是通过松弛操作逐渐降低权重。

还有著名的 Dijkstra 算法，其要求所有边的权重都为非负。其利用了贪心算法的思想，每次都选择最短路径。

LEC 13 全成对最短路径

全点对最短路径

全点对最短路径问题是从任一结点到其余结点的最短路径的问题。

如果不存在负值权重的边，可以用 Dijkstra 算法对每个结点进行操作。

还有一种利用动态规划思想的 Floyd-Warshall 算法，其要求可以存在负值权重的边，但不可以存在负值回路。

算法上课内容总结